Loan and Mortgage Maths

All examples are based on an initial mortgage/loan value of 200,000 (the maths is independent of currency).


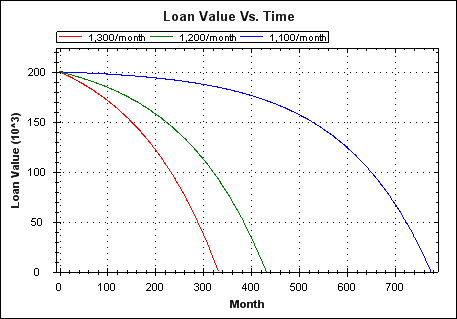
The remaining value of a loan throughout its life for three different monthly repayments. Interest rate is 6.5%.





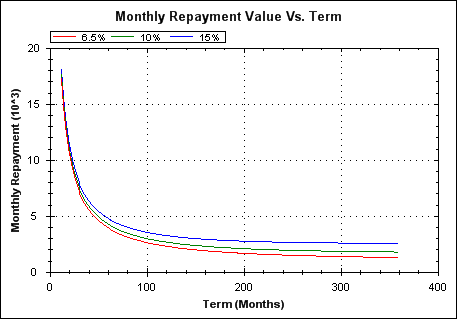
The relationship between term duration and repayment amount. Small increases in repayment can reduce term length by a lot.





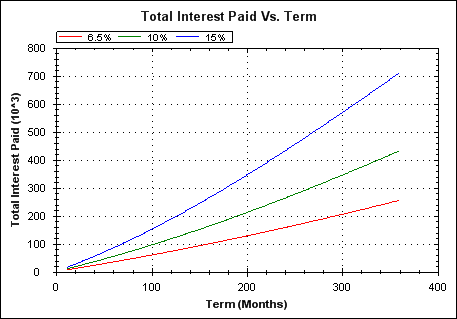
Total interest paid at end of mortgage life (on top of the 200k loan amount itself), versus term length. Plots shown for interest rates of 6.5, 10 and 15%. On a standard 25(UK)-30(US) year mortgage you're probably paying back at least the loan amount again in interest.





Mortgaging to the extremes of your ability to repay means that:

1. You're signing a lot more of your earned wealth over to the bank than if you took on a more manageable loan. Interest rates matter but are ultimately unknowable for the full life of a 25-30 year mortgage.
2. You're closer to the point of loan default in the event of a drop in earnings and/or a rise in interest rates.

Above all, don't trust advice from a bank; generally speaking they are not acting in your best interests but those of their shareholders. If you need advice then use an independent adviser that's not earning commission from each sale.

---

Derivations

Initial Discussion

A loan can be represented mathematically as two separate and independent pots of money:

(1) The initial loan amount (the loan principal) with no repayments, and therefore growing in value (increased debt) over time in line with the loan interest rate.

(2) The repayments considered as payments into a savings account with the same rate of interest as the loan. This savings pot will grow over time with the accumulation of payments and the compound interest on those payments.

The compound interest based growth of the savings pot exactly represents the effect of making repayments against the growing loan principal pot. I.e. e.g. early repayments make a more significant contribution to reducing and repaying the loan than later payments.

Key Variables

$P$	Loan principal amount.
$n$	Term length in months, i.e. the number of monthly payments after which the loan is paid off.
$r$	Monthly interest rate expressed as a ratio, e.g. 1.01 represents 1% interest per month.
$q$	Monthly interest rate expressed as a growth rate, e.g. 0.01 represents 1% interest per month, i.e. $r = 1 + q$
$a$	Fixed monthly payment.

Consider the principal amount independently of the repayments (pot 1); without repayments the total amount of debt grows each month.

$D_i$: Total debt at month $i$, assuming no repayments (here, debt is expressed as a positive value, growing over time).

$$D_i = P \cdot r^i \tag{1}$$

Now consider the monthly repayments independently of the loan, i.e. as payments into a savings account with the same monthly interest rate as the loan (pot 2).

$S_i$: Total value of saving pot at month $i$, assuming no initial savings.

$$S_i = \frac{a(1-r^i)}{1-r} \tag{2}$$

Noting that equation (2) is the formula for the sum of the first $i$ terms of a geometric series.

Loan balance (i.e. remaining debt) at month $i$ is given by subtracting debt at month $i$ from savings at month $i$.

$V_i$: Loan balance at month $i$ (here, a negative value for $V_i$ represents debt).

\begin{align} V_i & = S_i - D_i \tag{3} \\\\ V_i & = \frac{a(1-r^i)}{1-r} - P \cdot r^i \tag{4} \\\\ \end{align}

The loan is paid in full at month $n$, at which point the loan balance reaches zero, i.e. $V_i = 0$ and $i = n$

\begin{align} 0 & = \frac{a(1-r^n)}{1-r} - P \cdot r^n \tag{5} \\\\ P \cdot r^n & = \frac{a(1-r^n)}{1-r} \tag{6} \\\\ \end{align}

Rearranging equation (6) to find the monthly payment $a$ required to pay off a loan with a given principal amount $P$, interest ratio $r$, and term length $n$.

\begin{align} \frac{a(1-r^n)}{1-r} & = P \cdot r^n \\\\ a(1-r^n) & = (1-r)(P \cdot r^n) \\\\ a & = \frac{(1-r)(P \cdot r^n)}{(1-r^n)} \tag{7} \\\\ \end{align}

Rearranging equation (6) to find the term length $n$ given principal amount $P$, interest ratio $r$, and repayment amount $a$.

\begin{align} P \cdot r^n & = \frac{a(1-r^n)}{1-r} \\\\ \frac{r^n}{1-r^n} & = \frac{a}{(1-r)P} \\\\ \frac{1-r^n}{r^n} & = \frac{(1-r)P}{a} \\\\ \frac{1}{r^n}-1 & = \frac{(1-r)P}{a} \\\\ \frac{1}{r^n} & = 1 + \frac{(1-r)P}{a} \\\\ \frac{1}{r^n} & = \frac{a + (1-r)P}{a} \\\\ r^n & = \frac{a}{a + (1-r)P} \\\\ n & = \log_r \left[ \frac{a}{a + (1-r)P} \right] \tag{8} \\\\ \end{align}

Rearranging equation (6) to find $P$ given interest ratio $r$, repayment $a$, and term length $n$.

\begin{align} P \cdot r^n & = \frac{a(1-r^n)}{1-r} \\\\ P & = \frac{a(1-r^n)}{(1-r)r^n} \tag{9} \\\\ \end{align}

Note that there is no closed form expression for finding $r$ given the other variables. To find $r$ a numerical method can be used; typically a root finding method is used such as the secant method.

To find $r$ using a root finding method we can apply the method to equation (4). I.e. the root of that equation is the value of $r$ at which $V$ equals zero, and this is the value of $V$ when the mortgage/loan is paid in full.

Interest Rates and Ratios

All of the above maths uses the interest ratio $r$ to represent the mortgage interest rate; this value represents the monthly interest rate as a ratio. An annual interest rate can be converted to its equivalent $r$ value as follows.

Typically an interest rate is represented mathematically by a proportion, e.g. 10% is represented by the proportion $0.1$, and the equivalent ratio is that value plus one.

$$r_{annual} = 1 + q_{annual}$$

The equivalent monthly interest rate (as a ratio) can be obtained by taking the twelfth root, i.e. the monthly geometric mean of the annual interest rate ratio.

\begin{align} r_{monthly} & = \sqrt[12]{r_{annual}} \\\\ r_{monthly} & = \sqrt[12]{(1 + q_{annual})} \\\\ r & = \sqrt[12]{(1 + q_{annual})} \\\\ \end{align}

Colin,
(some time in 2009)
Derivations revised June 1st, 2019.

---