Fractional Brownian Motion

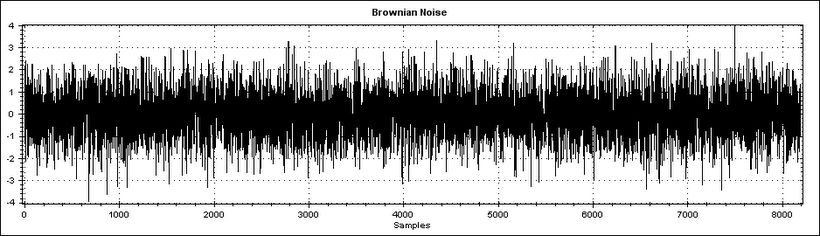
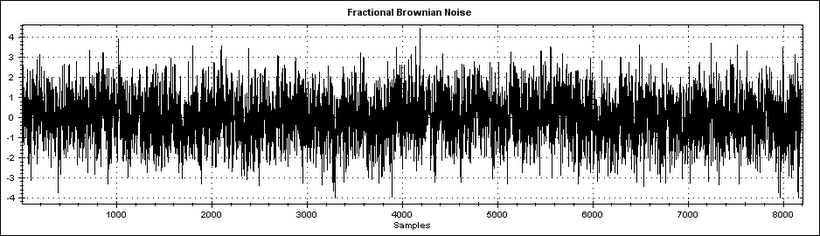
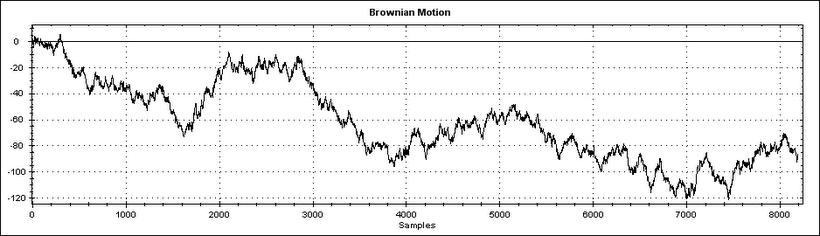
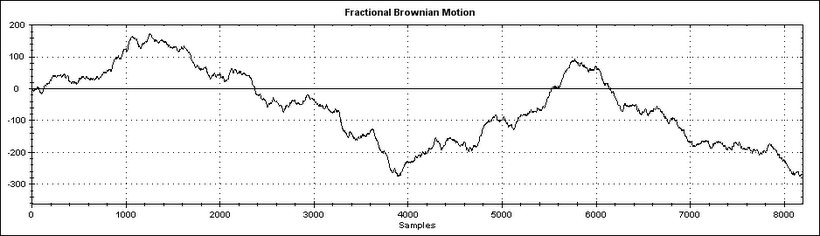
Each plot shows 8000 samples. As the number of samples increases (as we zoom out) the brownian noise plot looks increasingly like a solid bar with straight edges, whereas the Fractional Brownian Motion(FBM) plot exhibits self-affinity, meaning it looks the same at any magnification (barring magnifications below a lower threshold).

FBM data was generated using the Hosking method with a Hurst parameter (H) of 0.7. For source code and an excellent thesis on FBM generation see Simulation of fractional Brownian motion, Ton Dieker.

The Hosking method is an exact method and as such has time complexity of O(N^2). The reason for this is that FBM exhibits long term dependence and therefore each new sample is dependent on all previous samples. Faster approximate methods exist, which is largely the subject of the linked thesis.

The hosking.c file was ported to C# and ranlib was substituted with the following project which contains a NormalDistribution class .NET random number generators and distributions, Stefan Troschuetz, 2007.

Colin,
(some time in 2008)